
 |
テープレコダーの電気回路をやさしく解説しています。 質問・要望は koukouisao@yahoo.co.jp へ |
交流回路のコンデンサーに流れる電流は1/4サイクル電圧より進む。
進むとは??
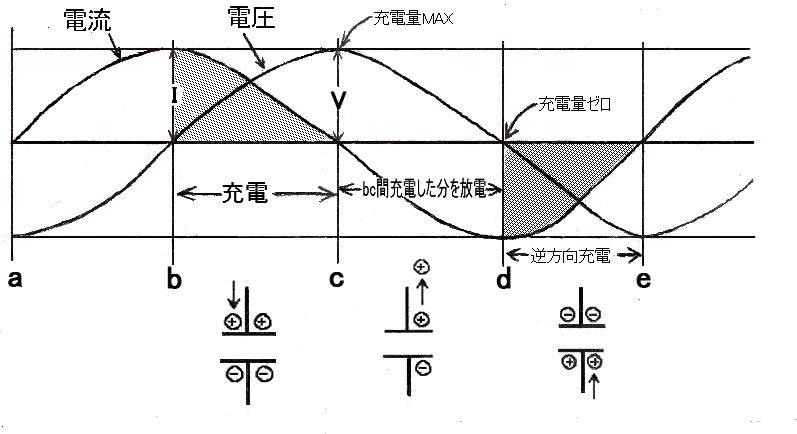 |
| 進むとか遅れると言う言葉を聞くとスタート点をゼロとして電圧と電流のどちらが早いかの様な連想 をしてしまう。 そういったことでは無くて、正弦波の電圧がコンデンサーに加えられてコンデンサーには電流が 流れている状態での電圧と電流がどの様になっているかを観測した時の話です。 (注1) コンデンサーに加える電圧が正弦波交流であれば、流れる電流も正弦波(正確には余弦波)になります。 同じ正弦波ですが1/4波長だけ電圧より進んだ波形となります。 この1/4波長電流が電圧に対して先行した正弦波になることを「電流は1/4サイクル電圧より進む」と 言っているのです。電流の変化のしかたが1/4サイクル電圧より進むのです 正弦波の電圧が最高値になる時電流値は0であり、電流値の最高値は電圧が 最高値になるより1/4周期早い位置になります。 これは(注1)の数式を見てわかる様にQ=CVで表されるコンデンサーの性質よるものです。 抵抗に正弦波を加えた場合はV=RIで示されるように電流は電圧に比例します。 ですから電圧が最高値になった時電流も最高値になります。 抵抗に流れる電流は進み遅れともに無しとなります。 コンデンサーの場合はコンデンサーに蓄えられた電荷の量と電圧が比例関係に有ります。 電流=「電荷が時間に対してどれだけ変化しているか」ということから電荷量を時間で微分した値。 Q=CVからCVの時間での微分値が電流になります。 この電圧の時間での微分値に比例すると言うことで電流が1/4サイクル進む結果となっているのです。 (注1) 電流は1秒間のコンデンサーに出入りする電荷変化量です。電圧をVm sin(2πft)とすると Q=C x Vm sin(2πft) 電流I=dQ/dt = 2πfC x Vm cos(2πft)電荷量Qの変化の速さが電流 ですので。変化する電荷量の時間での微分値が電流になります。 |