ハノイの塔を攻略せよ！

概要：再帰呼び出しを使うアルゴリズムとして超有名な「ハノイの塔」を詳細に解説します。

C言語の習得における最大の難関であると言っても過言ではない再帰呼び出し。
2年前、プログラム自体初心者だった私がC言語を学んでいたあの頃、
「明解C言語」の内容はほぼ完璧に理解できたというのにどうしても再帰だけは、
これだけはいまいちピンと来なかった……。

もちろん、全くわからなかったわけじゃーない。
どのような動作をするのか、どのようなときに使うのが有効か、
それくらいはわかった。

なんとなく読める……でも書けない。
そんなレベルだった。

理解できないままプログラムの勉強は続けたが、
殆ど困ることはなく、必要性さえ疑わしい今日この頃。
もしかしたら絶滅したりして！？って言うか、して下さい……(泣)。
みたいなことを願いつつ、やっぱり再帰だけ理解できないのは悔しい！
という思いもあり……。

そんな折、「月刊アスキー」にハノイの塔の解説記事が掲載された。
2年越しの雪辱を晴らすため、このページだけは真剣に読んだ私。
そうしたら……わかったー(笑)！
わかっちゃったよ、やったー！

というわけで、長い前置きですみません。
今回は、今度こそ本気で再帰を理解しようとする方の一助となるように
「ハノイの塔」のアルゴリズムについて詳しく解説します。

■ハノイの塔

地面に棒を3本立てて、左から順に A、B、C と呼ぶことにする。
棒Aに穴の空いた円盤を何枚か重ねてはめておく。
円盤のサイズは、それぞれ異なり、大きい円盤の上に小さい円盤を載せる。
円盤の枚数を3枚とすれば、下図のようになる。

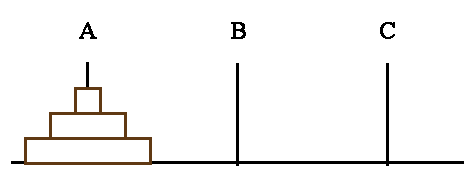
パズルの内容は、棒Aにある全ての円盤を棒Cに移動すること。
ただし、以下のルールを守らなければならない。

■ルール

・一度に1枚だけ円盤を移動する。
・小さい円盤の上に大きな円盤を載せてはいけない。
・棒A、棒B、棒C以外の場所に円盤を置いてはならない。

■再帰を理解するコツ

再帰は処理の流れを追うのが非常に困難です。
for文みたくループが一周するたびに制御変数の変動を考え、処理を理解する方法は通じません。

そもそも再帰の利点は「繰り返し処理をスマートに記述する」ことであり、
「人間の大まかな考えをそのままプログラムに置き換えられる」ことです。
細かい事を考えるのはナンセンスなんですね。

再帰を理解するのに大切なこと……それはイメージを掴むこと。
途中経過はブラックボックスのままで構いません。
ただ、どういう処理を繰り返したいのかということだけを考えれば良いのです。

もし深いところへ行っちゃったあなたは……戻ってきて下さい(笑)。
深追いせず、イメージを掴むことを決して忘れず、以降の解説をお読み下さいませ。

■3枚の円盤を移動する手順



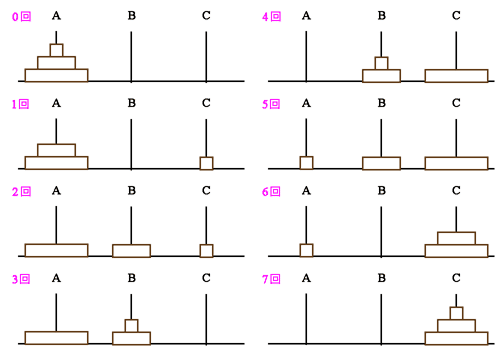
個々の移動規則は見つけられましたか？
ダメですよ、見つけようとしては(笑)。
そうやって、深いところへ行ってしまったあなたは戻ってきて下さいね。

ここで重要なのは「3回」の時です。
移動させるべき3枚の円盤の中から
2枚の円盤を棒Aから棒Bに移動させた状態ですね。

同様に「5回」の時は……
移動させるべき2枚の円盤の中から
1枚の円盤を棒Bから棒Aに移動させた状態ですね。

つまり……
「移動させる円盤が n 枚ならば、
まずは n-1 枚を棒Aから棒Bに移動しておかなければならない。」
という法則が成り立つのです。

そこに至るまでの過程は無視して下さい。

あと、もう一つ重要なのは、
「n-1 枚の円盤を棒Aから棒Bへ移動する場合と
棒Bから棒Aへ移動する場合は交互に訪れる。」
という法則です。

1回から3回、4回から5回までの目標は「一番下の円盤を棒Cに移動する」事ですが、
その為には上に載っている全ての円盤を、空いている棒へ移動させなければなりません。
今、棒Aに移動させる円盤があるのならば、棒Bが空いているはずです。
だから、上に載っている円盤を全て棒Bへ移動させます。
そして次の瞬間から棒Bに移動させるべき全ての円盤があることになり、
棒Aが空いていることになります。
したがって、上に載っている円盤を全て棒Aへ移動させます。
以降も同じ事の繰り返しです。

この考えが方が非常に重要です。
もう一度まとめてみると以下の繰り返しであることがわかります。

１．一番下の円盤を棒Cへ移動させたい。
２．その為に上に載っている全ての円盤を空いている棒(A or B)に移動させる。
３．一番下の円盤を棒Cへ移動させる。

これで、1枚の円盤を棒Cへ移動させたことになります。
移動させるべき残りの円盤は n-1 枚です。

■プログラムで表現する

それでは、プログラムで円盤の移動を表現してみましょう。
円盤を移動させると言っても配列などで表現するわけではありません。
"AからCへ"といった文字列を表示するだけです。

移動は後で考えるとして、関数の原型から決めましょう。

void Hanoi(int n,char *from,char *work,char *dest);

n　…　移動させる円盤の枚数
from　…　移動元の棒の名前
work　…　作業用に使う棒の名前
dest　…　移動先の棒の名前

この関数の意味するところは「第二引数から第四引数へ n 枚の円盤を移動させろ」
ということになります。

注意して欲しいのは、必ずしもA棒に円盤があるとは限らないことです。
しかし、from には円盤があります。
そうなるように再帰呼び出しを行うのですから。
というわけで、どの変数がどの棒の名前を指しているかはあまり気にしないで下さい。
抽象的な方が理解しやすいです。
また、何番の円盤を移動させるのかも取り敢えずは考えないことにして下さい。

■main 関数からの呼び出し

移動させる円盤は3枚、
移動元をA棒、移動先をC棒、作業棒をB棒とすれば
main 関数からの呼び出しは次のようになります。

Hanoi(3,"A","B","C");

■円盤を一枚移動させる

移動元は from 、移動先は dest でしたから、
"from から dest へ"という文字列を表示させればいいことになります。

printf("%s から %s へ\n",from,dest);

この時、度重なる再帰呼び出しによって from や dest の指すものが、
最初の from や dest とは異なっているかも知れませんが、
全く気にする必要ありません。
その時移動させたい円盤が from にあり、
その移動先が dest にあるように再帰呼び出しを行うのですから、
それぞれには適当なものが入っているのです。

■一番下の円盤を移動させるまで

一番下の円盤を移動させるためには
上に載っている全ての円盤( n-1 枚)を空いている棒に移動させなければなりません。

これは単純に以下のようなプログラムで表現します。

Hanoi(n-1,from,dest,work);

始めは第二引数に円盤が積まれているのですから、
上に載っている n-1 枚の円盤を第三引数に移動させればいいんでしたよね。

■いつまで繰り返すのか？

再帰呼び出しをいつまで繰り返すのかも理解に苦しむ点です。
それを理解するためには関数全体を見なければなりません。

関数は次のようになっています(一部省略)。

void Hanoi(int n,char *from,char *work,char *dest)
{
　　if(？) Hanoi(n-1,from,dest,work);

　　printf("%s から %s へ\n",from,dest);

　　……
}

見るべきは printf を実行するタイミング、
つまり、円盤を移動させるタイミングです。

この関数は、？の条件が成り立つ限り再帰呼び出しを続けます。
そして、？の条件が成り立たなくなった場合に円盤を移動させます。

ということは、Hanoi 関数の第一引数に渡す、移動させる円盤の枚数は1枚以上でなければなりません。
0枚の円盤を移動させる再帰呼び出しの中で更に再帰呼び出しが起きないことはもちろんですが、
移動させる枚数が0枚なのに printf を実行して、円盤を移動させてはマズイのです。

というわけで、？は n-1>=1 つまり n>=2 です。

void Hanoi(int n,char *from,char *work,char *dest)
{
　　if(n>=2) Hanoi(n-1,from,dest,work);

　　printf("%s から %s へ\n",from,dest);

　　……
}

ここでもイメージが重要です。
一行目で「上に載っている全ての円盤を移動させて下さい。」とお願いして、
それが終わったら二行目で「残っている一番下の円盤を移動させて下さい。」とお願いしているのです。
かなりアバウト指示ですが、
「人間の大まかな考えをそのままプログラムに置き換えられる」のが再帰の利点でしたね。

■同じ事を繰り返せ

この関数にはまだ三行目があります。
三行目のプログラムは一行目とよく似ているのですが、意味が異なります。
一行目は上に載っている円盤を移動させることが目的でした。
そして二行目で一番下の円盤を移動させました。
あとは同じ事を繰り返せばいいので、
三行目では main 関数から呼び出した時みたいに指示します。

今、移動させるべき円盤は一枚減り、n-1 枚になりました。
円盤は先ほど work だった棒にあります。
というわけで、最初にやったように第二引数から第四引数へ
全ての円盤( n-1 枚)を移動させるように指示します。

Hanoi(n-1,work,from,dest);

一行目の n-1 とは意味が異なる点に注意して下さい。
今度は一番下の円盤も数えて n-1 枚しかないのです。

また、work と from の場所が一行目とは異なりますが、
反転している、という事だけが重要です。
理論のところでも言いましたが、
移動させるべき全ての円盤はA棒とB棒を交互に移動するのでしたね。

再帰呼び出しの動作を考えれば、
これらの変数にどの棒の名前が入っているか分かるかも知れません。
でも考えないで下さい。
ただ、反転しているという事だけが重要なのです。

再帰呼び出しを行う条件は一行目と同じです。
0枚の移動は有り得ないということです。

void Hanoi(int n,char *from,char *work,char *dest)
{
　　if(n>=2) Hanoi(n-1,from,dest,work);

　　printf("%s から %s へ\n",from,dest);

　　if(n>=2) Hanoi(n-1,work,from,dest);
}

■完成プログラム

#include<stdio.h>

void Hanoi(int n,char *from,char *work,char *dest)
{
  if(n>=2) Hanoi(n-1,from,dest,work);

  printf("%d を %s から %s へ\n",n,from,dest);

  if(n>=2) Hanoi(n-1,work,from,dest);
}

int main(void)
{
  Hanoi(4,"A","B","C");

  return 0;
}

void Hanoi(int n,char *from,char *work,char *dest)
{
    if(n>=1){
        Hanoi(n-1,from,dest,work);

        printf("%d を %s から %s へ\n",n,from,dest);

        Hanoi(n-1,work,from,dest);
    }
}

int main(void)
{
    Hanoi(4,"A","B","C");

    return 0;
}

#include<stdio.h>

void Hanoi(int n,int x,int y)
{
    if(n>=2) Hanoi(n-1,x,6-x-y);

    printf("%d を %d 軸から %d 軸へ\n",n,x,y);

    if(n>=2) Hanoi(n-1,6-x-y,y);
}

int main(void)
{
    Hanoi(3,1,3);

    return 0;
}

戻る　/　ホーム