しかし、大学の教科書に載っているような複雑な数式をプログラムで表現しようとすると、
始めは戸惑うかもしれません。
今回はちょっとだけ複雑な「ラグランジュの補間法」を例に
数式をプログラムで表現する基礎を解説します。
■ラグランジュの補間法
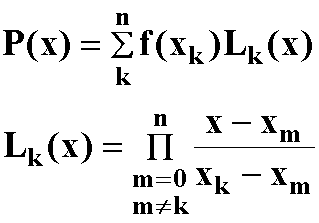
P(x) …… 求める値
xk …… 既知
f(xk) …… 既知
Lk(x) …… ラグランジュの補完係数
■言語
たとえ API プログラムで利用するのが目的でも
最初はC言語やC++言語を使って開発しましょう。
API で数値を表示させるのは面倒ですし、
API でしか通用しない関数や型などを絶対に使わない為でもあります。
■型
数学の世界で扱うのは実数です。
したがって、計算には int 型ではなく double 型を使いましょう。
■どこから作るのか?
数式をプログラムで表現する場合、
最後の式からプログラムを組み立てていきます。
「ラグランジュの補間法」の場合は P(x) が最後の式です。
したがって、P(x) の関数から作っていきましょう。
■事前に計算しておく必要がある値は関数に
Lk(x) は P(x) を計算する前に計算しておく必要があります。
しかし、本当に先に計算するようなプログラムを組むのではなく、
Lk(x) は関数として P(x) の式から呼び出すようにしましょう。
■添字のある値は配列に
xk は x0 x1x2 … xk … xn の事です。
これはどこかで見たことがありませんか?
そう、配列ですね。
配列として xk を表現すれば x[0] x[1] x[2] … x[k] … x[n] と書けます。
■ソースファイル
数式のような汎用的な関数は main 関数のあるソースファイルとは別の
独立したソースファイルに書きましょう。
■P 関数
P(x) の式が必要とする値は x だけです(xk と f(xk) は既知)。
Lk(x) 式が必要とする値も x だけです。
他は外部から与える必要はありませんので、
唯一外部に公開される P(x) 関数に与えるべき値は x だけということになります。
また、Lk(x) は関数にします。
double x[]={-4,-1, 7, 8, 9};
double f[]={-5, 6, 3, 2,-1};
int N=sizeof(x)/sizeof(x[0]);
double P(double xx)
{
int n=N-1;
double d=0;
for(int k=0;k<=n;k++)
d+=f[k]*L(k,xx);
return d;
}
N はデータの個数です。
n はデータの個数ではなく、最後のデータの添字です。
数式を見ると k=0 から n までの範囲を加算しています。
この時 n は含まれるので、for 文の条件式は n 以下にしました。
もっとプログラムらしく N 未満などと書くこともできます(n は整数だから)。
■分点間隔
ところで、k の間隔はいくつでしょうか?
数式を見てもどこにも書いてありません。
1 でしょうか? 0.1 でしょうか?
答えは「必要な精度が得られる」間隔です。
今は必要な精度が分からないので、間隔は 1 ということにしておきましょう。
■L 関数
Lk(x) が必要とするのは k と x の値です。
double L(int k,double xx)
{
int n=N-1;
double d=1;
for(int m=0;m<=n;m++)
if(m!=k)
d*=(xx-x[m])/(x[k]-x[m]);
return d;
}
if 文には注意が必要です。
m!=k という条件式を for 文の中に書いてはいけません。
m!=k という条件が成り立たなくても m の値を一つ進めてまだ計算を続けるからです。
もし for 文の中に書いたら、m!=k がループの終了条件になってしまいます。
■ヘッダーファイル
外部に公開する必要があるのは P 関数だけです。
本当ならば xk と f(xk) も外部から与えるべきですが、それは自分で考えて下さい。
一つだけ言わせてもらえば、外部に公開するグローバル変数は使わない方が良いです。
double P(double xx);
■まとめ