テトリスの作り方(其の一)
概要:自作プログラム『SPACE TETRIS』の作り方を丁寧に解説!
ゲーム好きのプログラマーなら誰しも作ってみたいと思うゲームの一つにテトリスが挙げられるでしょう。
でも自分で作るとなると分かりそうで分からなくって……尻込みしちゃいませんでしたか?
何を隠そう私はしました(笑)。
そんな時に出会ったのが【Windowsゲームプログラミング/赤坂鈴音】です。
ここに載っていた“かなり割り切った”仕様のテトリスがブレークスルーとなりました。
私が作った『SPACE TETRIS』のデータ構成は
Windowsゲームプログラミングのサンプル(以降は単にサンプル)のそれを継承しています。
ですので、プロフェッショナルなものではなく、
テトリスやその他の落ち物ゲームの基本的な考え方が分かる程度のものとお考え下さい。
この“かなり割り切った”データ構成の「制約」を除外しようと思うとかなり大変なことになりそうです。
しかし、『SPACE TETRIS』が簡素なプログラムだったサンプルと同じかというと
殆ど別物というくらい色々やっています。
「制約」の範囲内で最大限頑張ったと言えるでしょう。
従って、難しく実践的な内容も含まれていることをご了承下さい。
ここで解説するのは『SPACE TETRIS』のプログラムですが、
一般的なテトリスや落ち物ゲームの基本的な考え方も身に付くものと思われます。
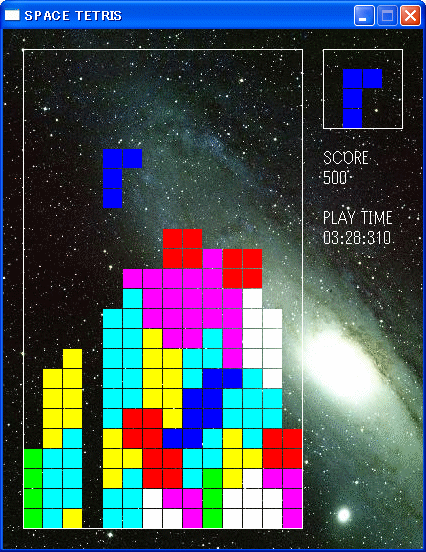
■SPACE TETRIS
とりあえず私が作ったプログラムで遊んでみて下さい。
遊び飽きたらいろいろ観察してみて下さい。
わざわざここで説明しなくても仕様が理解できるはずです。
実行ファイル、その他
■データ構成
私はゲームをプレイしていてあまり気にした事がありませんでしたが、
落ちてくるピース(ブロックの集合)やブロックが積まれていくゲームフィールドは
一定の大きさを持った(例えば、横20ピクセル、縦20ピクセル)
マス(と呼ぶ事にします)を最小単位として管理しています。
もしマスを用いないとすると……
画素を調べることによってブロックの有る無しを判定することになりそうですが、あまり利口とは言えませんよね?
マスを一つの変数に対応させて……
全体としてはブロックの有る無しを記録する配列を調べることによって様々な操作を実行するのです。
それではそれぞれの配列を定義してみましょう。
今回は簡単化のためによく使う変数はグローバル変数にしています。
本当はグローバル変数は極力使わないのが鉄則ですので、気になる方は直してみて下さい。
// ピースの横と縦のマス数
#define PIECE_WIDTH 4
#define PIECE_HEIGHT 4
/* フィールドの横と縦のマス数 */
#define FIELD_WIDTH 14
#define FIELD_HEIGHT 24
// マスのピクセル数
#define CELL_WIDTH 20
#define CELL_HEIGHT 20
BYTE field[FIELD_WIDTH][FIELD_HEIGHT]={0}; /* ゲームフィールド */
DWORD fColor[FIELD_WIDTH][FIELD_HEIGHT]={0}; // ゲームフィールドの色
BYTE piece[PIECE_WIDTH][PIECE_HEIGHT]={0}; /* 現在移動中のブロック */
DWORD pColor[PIECE_WIDTH][PIECE_HEIGHT]={0}; // 現在移動中のブロックの色
POINT location={0,0}; /* 現在移動中のブロックの位置 */
BYTE next[PIECE_WIDTH][PIECE_HEIGHT]={0}; // 次のブロック
DWORD nColor[PIECE_WIDTH][PIECE_HEIGHT]={0}; // 次のブロックの色
/* …… */ はサンプルにもともとあったコメント(ちょっと変えた箇所有り)、
// …… は私が附したコメントです。
今回はブロックに色をつけるので、
それぞれのブロックの色を記録する配列も必要です。
また、次のブロックをプレイヤーに提示するために
これも配列として用意しておく必要があります。
現在移動中のピースの位置を示す POINT 型変数 location も見逃さないで下さい。
location が記録するのは「ピースの左上がどこのマスにあるか」です。
これについては後ほど詳しく解説します。
さて、このデータ構成を与えることによって、
分かる人にはテトリスの作り方の全てが分かっちゃったかも知れません。
それ程にデータ構成は重要で絶対です。
今回はこの制約の多いデータ構成を用いて頑張ることにしましょう。
■座標系
座標の原点はウィンドウの左上です。
右にいけば x が大きくなるし、下にいけば y が大きくなる一般的な座標系です。
では配列はどうか?
これは描画の仕方次第ですが、
配列についても [0][0] という添字を持つ要素は左上を表していることにしましょう。
また、マスを最小単位として構成される座標系をマス座標と呼ぶことにします。
■ピースを作る
今回作るピースは7種類です。
□を空白、■をブロックとしてそれぞれのピースを表すと以下のようになります。
色は適当に決めたので、あなたの好みで変えて下さい。
0 1 2 3 4 5 6
□□□□ □■□□ □□□□ □□□□ □□□□ □□□□ □□□□
□■■□ □■□□ □■□□ □■■□ □■■□ □□■□ □■□□
□■■□ □■□□ □■■□ □■□□ □□■□ □■■□ □■■□
□□□□ □■□□ □■□□ □■□□ □□■□ □■□□ □□■□
CreatePiece() 関数はピース作りを担当しています。
作成先が次のピースであることに注意して下さい。
// 次のブロックをあらかじめ作っておく
void CreatePiece(void)
{
for(int y=0;y<PIECE_HEIGHT;y++){
for(int x=0;x<PIECE_WIDTH;x++){
next[x][y]=0;
nColor[x][y]=0;
}
}
switch(rand()%7){
case 0:
next[1][1]=1; next[2][1]=1; next[1][2]=1; next[2][2]=1;
nColor[1][1]=nColor[2][1]=nColor[1][2]=nColor[2][2]=0x000000ff;
return;
case 1:
next[1][0]=1; next[1][1]=1; next[1][2]=1; next[1][3]=1;
nColor[1][0]=nColor[1][1]=nColor[1][2]=nColor[1][3]=0x0000ff00;
return;
case 2:
next[1][1]=1; next[1][2]=1; next[2][2]=1; next[1][3]=1;
nColor[1][1]=nColor[1][2]=nColor[2][2]=nColor[1][3]=0x0000ffff;
return;
case 3:
next[1][1]=1; next[2][1]=1; next[1][2]=1; next[1][3]=1;
nColor[1][1]=nColor[2][1]=nColor[1][2]=nColor[1][3]=0x00ff0000;
return;
case 4:
next[1][1]=1; next[2][1]=1; next[2][2]=1; next[2][3]=1;
nColor[1][1]=nColor[2][1]=nColor[2][2]=nColor[2][3]=0x00ff00ff;
return;
case 5:
next[2][1]=1; next[1][2]=1; next[2][2]=1; next[1][3]=1;
nColor[2][1]=nColor[1][2]=nColor[2][2]=nColor[1][3]=0x00ffff00;
return;
case 6:
next[1][1]=1; next[1][2]=1; next[2][2]=1; next[2][3]=1;
nColor[1][1]=nColor[1][2]=nColor[2][2]=nColor[2][3]=0x00ffffff;
return;
}
}
CreatePiece() 関数は NextPiece() 関数から呼び出されます。
NextPiece() 関数は次のピースを現在のピースとしてコピーして、
さらに次のピースを作ります。
次のピースがなければ(ゲーム開始直後)次のピースを作ってから同様の処理を実行します。
そして現在のピースの初期位置も設定します。
/* 次のブロックへ */
void NextPiece(BOOL first) // first:ゲーム開始から最初の呼び出しか否か
{
if(first) CreatePiece();
for(int y=0;y<PIECE_HEIGHT;y++){
for(int x=0;x<PIECE_WIDTH;x++){
piece[x][y]=next[x][y];
pColor[x][y]=nColor[x][y];
}
}
location.x=5;
location.y=-3;
CreatePiece();
}
■ピースを移動する
ここで重要なのは移動先が有効な領域であるか?ということ。
具体的には次の事をチェックします。
○移動先はゲームフィールド内である
○移動先のマスは空いている
この役割を担っているのがMovePiece() 関数ですが、下請けとして
ピースの一番左のブロック位置を返す関数として GetPieceLeft() 関数、
ピースの一番右のブロック位置を返す関数として GetPieceRight() 関数
ピースの一番下のブロック位置を返す関数として GetPieceBottom() 関数
を定義して、呼び出しています。
まずはこれらの関数の定義を見てみましょう。
また、MovePiece() 関数では使いませんが、
ピースの一番上のブロック位置を返す関数として GetPieceTop() 関数
も定義しています。
// エラー
#define ERR -1
/* piece[][] 内のブロックの最上部の位置を返す */
int GetPieceTop(void)
{
for(int y=0;y<PIECE_HEIGHT;y++){
for(int x=0;x<PIECE_WIDTH;x++){
if(piece[x][y]){
return y;
}
}
}
return ERR;
}
/* piece[][] 内のブロックの最下部の位置を返す */
int GetPieceBottom(void)
{
for(int y=PIECE_HEIGHT-1;y>=0;y--){
for(int x=0;x<PIECE_WIDTH;x++){
if(piece[x][y]){
return y;
}
}
}
return ERR;
}
/* piece[][] 内のブロックの左側の位置を返す */
int GetPieceLeft(void)
{
for(int x=0;x<PIECE_WIDTH;x++){
for(int y=0;y<PIECE_HEIGHT;y++){
if(piece[x][y]){
return x;
}
}
}
return ERR;
}
/* piece[][] 内のブロックの右側の位置を返す */
int GetPieceRight(void)
{
for(int x=PIECE_WIDTH-1;x>=0;x--){
for(int y=0;y<PIECE_HEIGHT;y++){
if(piece[x][y]){
return x;
}
}
}
return ERR;
}
これらの関数は 0 〜 3 の値を返します。
例えば GetPieceLeft() 関数が 0 を返せば
現在移動中のピースの x 位置 location.x より 0 個右に左端のブロックがあるということになります。
location はピースの左上がどこのマスに対応しているかを記録しています。
■location
location が指す位置が把握できないとプログラムを理解することができないので
ここでちゃんと説明しておきましょう。
例えば、次のピースが現在移動中だったとします。
□□□□
□■□□
□■■□
□■□□
ここで location が指すのはピースの左上のマス座標です。
ゲームフィールドと現在のピースをマス座標で表現すると以下のようになり、
この時、location.x = 3 , location.y = 2 です。
0 13
0 □□□□□□□□□□□□□□
1 □□□□□□□□□□□□□□
2 □□□□□□□□□□□□□□
3 □□□□■□□□□□□□□□
4 □□□□■■□□□□□□□□
5 □□□□■□□□□□□□□□
6 □□□□□□□□□□□□□□
7 □□□□□□□□□□□□□□
8 □□□□□□□□□□□□□□
9 □□□□□□□□□□□□□□
10 □□□□□□□□□□□□□□
11 □□□□□□□□□□□□□□
12 □□□□□□□□□□□□□□
13 □□□□□□□□□□□□□□
14 □□□□□□□□□□□□□□
15 □□□□□□□□□□□□□□
16 □□□□□□□□□□□□□□
17 □□□□□□□□□□□□□□
18 □□□□□□□□□□□□□□
19 □□□□□□□□□□□□□□
20 □□□□□□□□□□□□□□
21 □□□□□□□□□□□□□□
22 □□□□□□□□□□□□□□
23 □□□□□□□□□□□□□□
それでは GetPieceLeft() が返す値はいくらでしょうか?
これらの関数は現在のピースに対して処理するのですから、返却値は 1 です。
同様に GetPieceRight() の返却値は 2
GetPieceBottom() の返却値は 3
GetPieceTop() の返却値は 1 です。
■ピースを移動する(続き)
MovePiece() 関数の定義は以下のようになります。
厳重に配列の添字チェックを行っているので見づらくなっていますが、
不正な領域にアクセスすると大変なことになるのでちゃんとやりましょう。
この関数の基本方針はとにかく移動不可のパターンを全て調べて、
それでもまだチェックをパスしていたら移動可能だと判定することです。
/* MovePiece 関数の引数 */
#define PIECE_LEFT 2
#define PIECE_RIGHT 4
#define PIECE_DOWN 8
/* ブロックの移動判定 */
// 戻り値:TURE(移動した) or FALSE(移動不可)
BOOL MovePiece(int move) // move:移動したい方向
{
int x,y,left,right,bottom;
switch(move){
case PIECE_LEFT:
left=GetPieceLeft();
if((location.x)+left <= 0) return FALSE;
for(y=0;y<PIECE_HEIGHT;y++){ // ↓(location.x)+x-1>=0 , (location.y)+y>=0
for(x=0;x<PIECE_WIDTH;x++){ // は添字の有効性を調べている
if(piece[x][y] && (location.x)+x-1>=0 && (location.y)+y>=0
&& field[(location.x)+x-1][(location.y)+y]){ // 一つ左にブロックがある
return FALSE;
}
}
}
location.x--;
return TRUE;
case PIECE_RIGHT:
right=GetPieceRight();
if((location.x)+right >= FIELD_WIDTH-1) return FALSE;
for(y=0;y<PIECE_HEIGHT;y++){ // ↓(location.x)+x+1<FIELD_WIDTH , (location.y)+y>=0
for(x=0;x<PIECE_WIDTH;x++){ // は添字の有効性を調べている
if(piece[x][y] && (location.x)+x+1<FIELD_WIDTH && (location.y)+y>=0
&& field[(location.x)+x+1][(location.y)+y]){ // 一つ右にブロックがある
return FALSE;
}
}
}
location.x++;
return TRUE;
case PIECE_DOWN:
bottom=GetPieceBottom();
if((location.y)+bottom >= FIELD_HEIGHT-1) return FALSE;
for(y=0;y<PIECE_HEIGHT;y++){ // ↓(location.y)+y+1>=0 , (location.y)+y+1<FIELD_HEIGHT
for(x=0;x<PIECE_WIDTH;x++){ // は添字の有効性を調べている
if(piece[x][y] && (location.y)+y+1>=0 && (location.y)+y+1<FIELD_HEIGHT
&& field[(location.x)+x][(location.y)+y+1]){ // 一つ下にブロックがある
return FALSE;
}
}
}
location.y++;
return TRUE;
}
return FALSE;
}
MovePiece() 関数はプレイヤーからの操作によってはもちろん、
プログラムからも一定時間ごとに下方向に移動するように呼び出されます。
1/4 次へ
戻る / ホーム
