高校数学勉強法
受験で数学を使うのなら、解き方の暗記はやめよう
数学の勉強についてどんなふうに考えていますか?
「数学っていくら勉強してもちっともできるようにならないんだよな。」、 「応用問題もやってるのに模試で点が取れないんだよな。」、 「解き方を忘れちゃうんだよなぁ。」という感じでしょうか。
問題文を読んでから1分もたたないうちに分からないとあきらめて解説を読み、 こんなこと分かるわけないよな~とぼやきながら解答を丸写しして勉強した気になっていませんか?
数学は覚えればできるというものではありません。漢字や英単語であれば「忘れた」「思い出せない」 「初めて見る単語だ」ということなら、すぐ辞書を引いて数回書き取り練習をして覚えようと努める。 これで十分勉強になるでしょう。
でも数学の場合は「分からない」「初めて見る問題だ」といって、 漢字や単語の勉強と同じようにすぐに答えを見てしまっては解けるようにはなりませんし、応用力も実践力もつきません。
ただ、中学生まではそのような勉強の仕方でも大丈夫だったのかもしれません。 高校でも定期テストくらいなら何とかなるでしょう。 でも、大学受験に数学を使うのであれば、到達したいレベルにもよりますが、 今すぐそのやり方を見直すべきではないでしょうか。
「量をこなす」はやめよう
では、どんなふうに勉強していけばいいのでしょうか。
定期試験が近づくと、とりあえず問題集の試験範囲部分を全部終わらせようと、 解答を書き写しているだけのような勉強を必死でやっている人はいないでしょうか?
ひたすら解答を書き写すだけのような勉強をするくらいなら、難しい問題は捨てて、 基本問題だけを完璧にするほうがよっぽど良い点がとれるはずです。
例えば、野球やテニスなどで素振りをするとき、 とにかくがむしゃらに回数をこなすことだけを考えてバットやラケット振るのと、 回数自体は少なくてもフォームや筋肉の使われ方などを意識しながら、 ボールが飛んできたことをイメージして1回1回時間をかけて振るのとではどちらが良いでしょうか。
数学の勉強も同じです。ただひたすら問題数をこなすことだけ考えて、分からなければすぐに答えを見て書き写し、 またすぐ次の問題へというのではなく、じっくり時間をかけて1つ1つの問題に取り組む必要があります。
図や表を書いたり、具体例を考えよう
分からないからといってすぐ答えを見るのではなく、問題文を何度も読み返し、図や表を描いてみたり、 具体的な数字で考えてみたりして、とにかくペンを動かしてください。紙が真っ白のままペンが止まっていては、 答えには一歩も近づけません。当たり前だし大したことじゃないと思っても、書いてみることで見えてくるもの、 気づくことがあるはずです。
ノートをきれいに使いたいのか、ノートには解答しか書きたくないという生徒も多々見受けられますが、 自分の考えたことや気づいたことを図やイメージとして書き出すことは、解くために必要なことですし、 数学の問題を解くときだけに必要なことでもありません。 ノートに書くのが嫌であれば、裏紙などを利用して考えやイメージをいっぱいに広げてみてください。
解答をすぐ見るのはやめよう
それでも分からないときはどうしたらいいでしょうか?
解き方のヒントや指針などが載っているのであれば、それを頼りにもう一度考えます。 それでも分からなければ、行き詰まった所だけちらっと解答を見てまた考える。 それでもどうしても分からなければ答えを読む。 理解したら、答えを写すのではなく解答は閉じて自力で答えを書いてみる。
問題集によっては、例題とその解説・解答がどーんとページの大半を占めていて、 下の方にその練習問題が載っているというものも多いですが、 例題の解答が問題のすぐ下に載っているからといってそれをすぐに読んではだめです。 例題も練習問題と同じように答えを見ずにじっくり取り組んでください。 例題を考えもせず解答を読んでしまっては数学の力はつきません。
もうだめだと思って解答を読んでみると、「こんなこと思いつくわけないよ!」とか、 「なんでこのことからこんなことが分かるの?」、「これ(この内容)どこから出てきたの?」 と思うこともあると思います。 それこそ、まだ考える量と時間が足りてない証拠です。考える時間を惜しんではいけません。 テストのように時間が限られているのではありませんから、たっぷり時間を使って考えてください。
とはいえ、数学だけ勉強しているわけにはいきませんよね。他の科目の勉強もしなければなりません。 そうなるとやはり考える時間が削られがちになってしまうでしょう。 それであれば、しばらく考えても分からない問題はとりあえず保留にしてみるのはどうでしょうか?
一生懸命考えたことは頭の奥の方に残っていますから、 ずっと考えているよりも一旦頭を切り替えて他の事をやってみたりすると、 ふとひらめくものです。リラックスしてお風呂に入っているときや、他の問題を解いているときなど、 ふとした時に「そういえばさっきの問題、こんなふうにしたら解けるんじゃないかな・・・」ということもあるでしょう。 または、別の日に改めてその問題を考えてみたらすんなり解けてしまったなんていうこともあると思います。
そんなことあるはずないと思う人は、さっきも書きましたが、考える時間が短すぎです。 実際私が高校生の頃、解答を見るのがイヤで粘って考えていると、 お風呂の中でふと別の考え方や解き方のアイディアを思いついたことが何度もありますし、 夜眠っていて夢の中で解き方のヒントを見つけたこともあります。
まずは、「もう少しで解けそうなんだけど」とか「途中までは解けたんだけど」という問題で試してみてください。 解けたときの感動はやる気と自信につながって良いサイクルを生み出すはずです。
公式は導き出し方も身につけよう
公式を忘れてしまったときどうしていますか?
「あっ、この問題は○○公式を使えばいいんだ!」ということは分かっても、その公式が思い出せない・・・ ということはよくあることでしょう。そんなとき、教科書や参考書、公式集などからその公式を探し出して、 ノートの端の方に赤で書いてカラフルに囲って、隣に「覚える!」なんてコメントをつけて終わりにしていないでしょうか? それで覚えられればよいのですが、書いて満足してしまってなかなか覚えられないでしょうし、 覚えてもすぐ忘れてしまうでしょう。
では、どうすればいいのでしょうか?覚えるべき公式の中には簡単に導き出せてしまうものも多くあります。 例えば数Ⅱの三角関数で習う2倍角や3倍角、半角の公式などは忘れたからといってすぐ調べるのではなく、 忘れるたびに加法定理から導き出してみてください。
こうすることでしっかり定着して、万一試験中に公式を忘れてしまっても素早く導き出せますし、 確信を持ってその公式を使うことができます。試験時間は限られていますからそんなことをすれば時間的にロスですが、 うろ覚え状態で公式を使っても、実際に公式を間違えていたり、 公式自体合っていたとしても自信がないため集中できず計算ミスを招いたり・・・ ということを考えれば、多少時間をかけても導き出して確実なものを使うほうがよいと思いませんか? あくまで忘れてしまった場合の話ですが。
簡単に導き出せる公式はそれでよいとして、導き出すのが大変な公式はどうでしょうか。 忘れてしまったらほとんどアウトですが、公式定着をはかるための対策はあります。
学校で新しい公式を習うとき、その証明を先生が丁寧に説明してくれるはずです。 そのとき居眠りをしていたり、ただノートに書き写すだけになっていて、 先生が「この公式は重要だから絶対覚えてください」などと言ったときだけ目を見開き、 ノートに「☆重要!」などと書いて授業を理解した気になっていないでしょうか?
公式が導かれる過程をしっかり理解し、自分で導き出せるようにしておくことは公式の定着のためだけでなく、 応用問題を解く上で重要になってきまし、公式の証明自体が問題となって出題されるときもあります。 導くのが大変な公式でも、忘れたときはただ公式を調べるのではなく、 その導かれる過程も一緒に見てみることが大切です。
基礎をしっかり固めよう
応用問題ができないのは、基礎がしっかりできていないのも理由の1つではないでしょうか? 基礎がきちっとできていればいくらでも応用が利くと思います。 例えば数Bで数列を習いますが(数列をまだ学習していない人は下の「イメージ」を参考にしてみてください。)、 次のような問題はどうでしょうか?
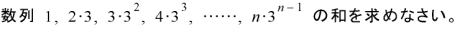
これは等差数列と等比数列の積の数列になっていて、よく例題でとりあげられているものです。 等差数列でも等比数列でもないのですから、等差数列の和の公式も、等比数列の和の公式も使えません。 ということは、どの公式も役に立たないから全くの別物としてこの例題の解き方を頭に叩き込むしかないのでしょうか?
新しい問題を見るたびに解き方を暗記というのでは正直苦しいです。一つ一つの問題が"点"でしかありません。 これでは記憶から消去されるのもあっという間、覚えきらず頭がパンクして嫌になるだけです。 しかし、この例題の解き方が等比数列の和の公式の導き出し方と同じだと分かるとどうでしょうか。 公式そのものが使えるわけではありませんが、使えないと思っていた公式とのつながりができましたね。
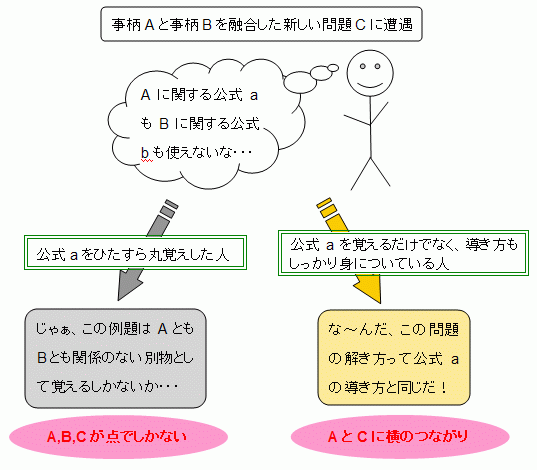
1つ1つの"点"でしかなかった公式と例題に横のつながりができました。 こうやって横のつながりができてくると、はるかに理解が深まり記憶にも残るのです。 等比数列の和の公式の導き出し方も上記の例題も教科書に載っているものですが、それぞれを別にしかとらえていないと、 基礎はあっても固まってはいないと言えるのではないでしょうか。 イメージで例えるなら、下の図のように基礎が固まっていない部分には応用が載ってこないという感じです。
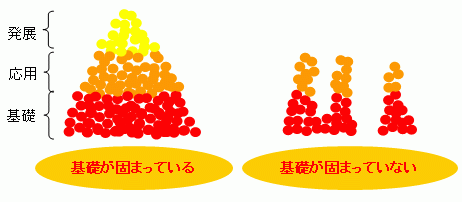
間違えた問題にマークをつけていこう
最後に、問題集はどう活用していったらよいでしょうか?
定期テスト前の部活休止期間になってから慌てて問題集をやり始め、 教科書から公式や同じような問題を探しだしてとにかく解き方を暗記する。 数学が得意な友達に出そうな問題を聞いて、とりあえず答えを丸覚えしようとする。 これでは、テスト中に公式を忘れた、解き方を忘れたとパニックになってほとんど白紙状態なんてことになりかねません。
部活が忙しいのは分かりますが、学校の授業で新しく習った事柄について、 問題集の基礎問題だけでもその週のうちにやるようにしてみてください。 その際、間違えた問題にチェックを入れていきます。「間違えたものや答えを見てしまったもの」、 「全く手がつけられなかったもの」、「解き方はあっていたけど計算ミスをしてしまったもの」など 2,3種類のマークを適当に決めて問題番号の脇に書き込んでおきましょう。
そして、定期テスト1週間前にマークのある問題を再度解く、標準問題に取り組む(マークをつけながら)。 テスト前日はマークのついた問題を中心に再度解く。これだけでも定期テストには十分対応できるでしょう。 また、受験勉強で問題集をやり直すとき、どの問題を復習すればよいのか、どういうところが出来ていないのかの目安になりますね。
それから、問題集の難易度についてですが、学校で勧められたからといって自分のレベルとかけ離れた問題集はお勧めできません。 自力では解けないけど答えを見れば理解はできるというのでは力はつきません。 答えを見れば分かる(答えを見ないとできない)問題ではなく、 時間はかかるけど頑張れば何とか答えを見ずにできるというレベルの問題集を選んでみてください。どんどん力がついていくはずです。
